A friend wanted to 3D-print a shape to demonstrate using calculus to find the volume of solids of known cross-section. The shape he wanted was a graph of $sin(x)$ vs $x^2$, where each vertical slice of the intersection was a square. Here's the graph, with $y_1 = sin(x)$ and $y_2 = x^2$. The blue lines show the edge of each square. He couldn't figure out how to do this in a CAD program (I'm not even sure if it's possible), so he asked me if I could write some code to render it.

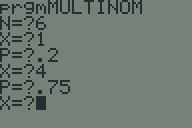
Another TI-BASIC challenge proposed to me by the same person who asked me last time was to calculate the probability mass function of a multinomial distribution. The formula is:

The naïve way of calculating this is to read $x\_1$ and $p\_1$ through $x\_k$ and $p\_k$ and then crunch the numbers. However, this necessitates a list to keep track of all the numbers and an extra loop at the end to crunch them. Since we don't actually need the numbers, there's an easier way.

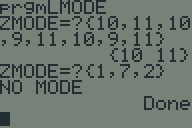
Recently, someone challenged me to write a program to find the mode (or modes) of a list in TI-BASIC. I picked up my TI-83+ and whipped this program up in about half an hour. Somebody else asked me for a copy, so I figured I'd post it on my website.