#!/usr/bin/env python
# This post was written as literate Python.
# ---
# title: Rendering a 3D shape with Python
# tags: ["Python", "OpenSCAD", "3D Printing", "Algorithm"]
# ---
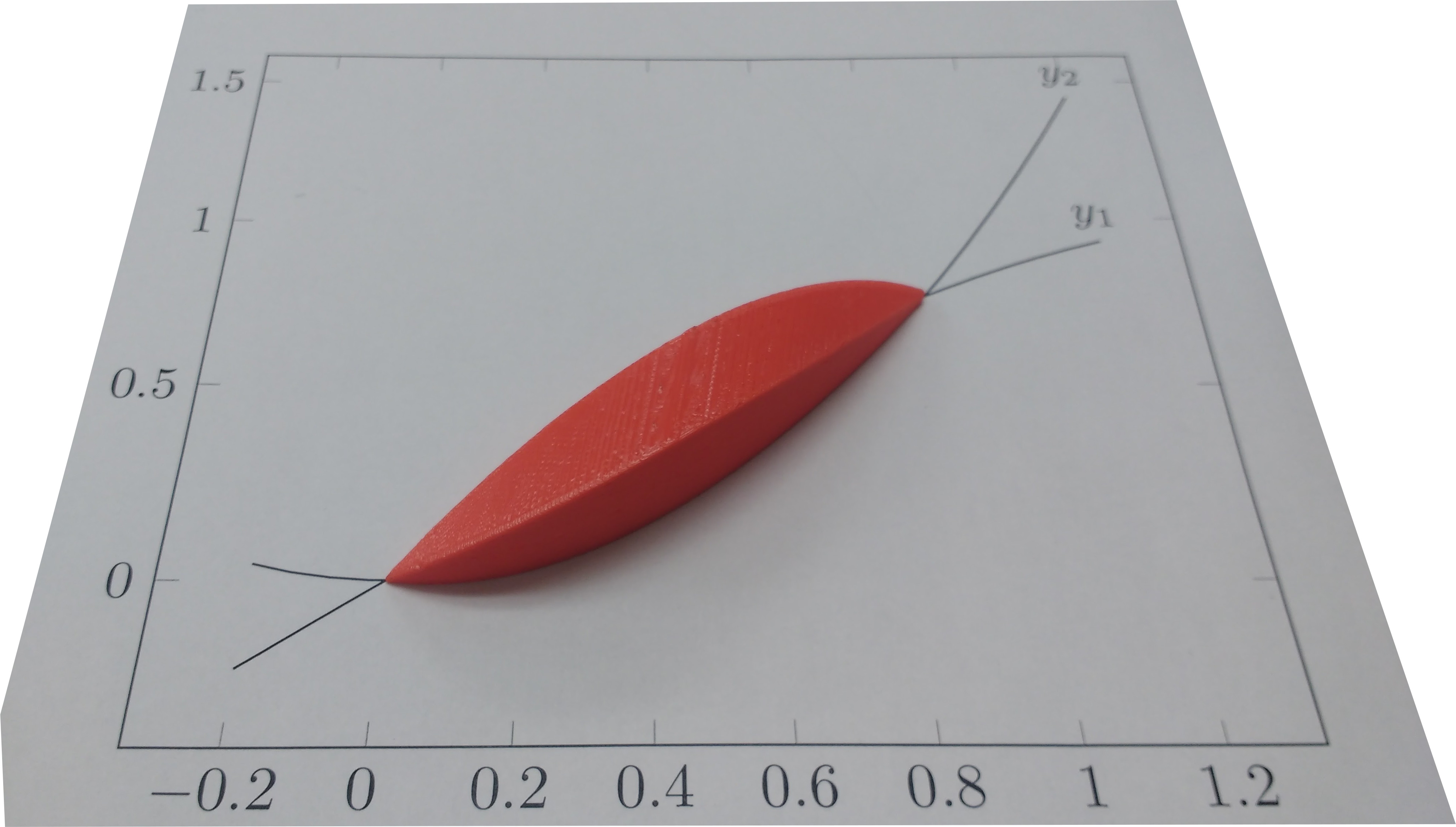
# A friend wanted to 3D-print a shape to demonstrate using calculus to find the volume of solids of known cross-section.
# The shape he wanted was a graph of $sin(x)$ vs $x^2$,
# where each vertical slice of the intersection was a square.
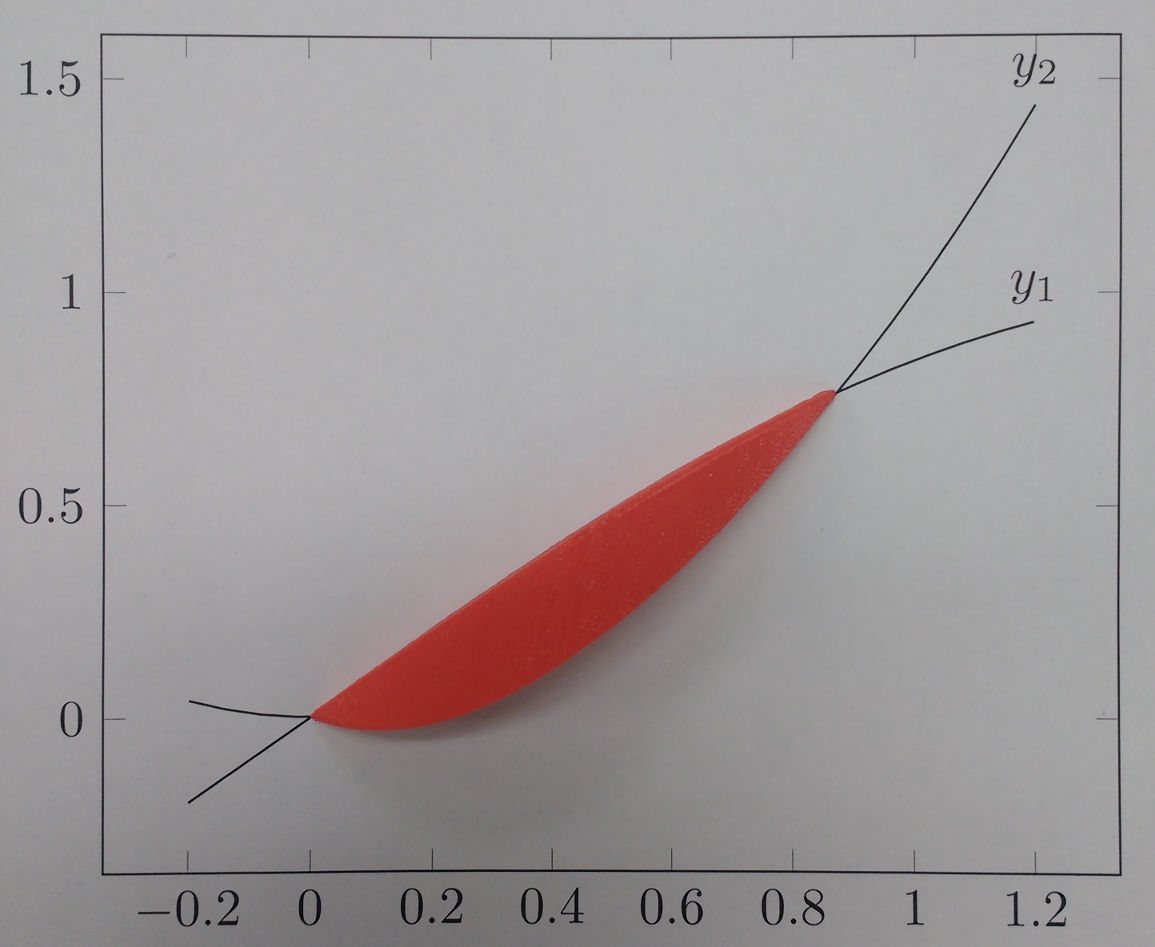
# Here's the graph, with $y_1 = sin(x)$ and $y_2 = x^2$. The blue lines show the edge of each square.
# He couldn't figure out how to do this in a CAD program (I'm not even sure if it's possible),
# so he asked me if I could write some code to render it.
#
# The first attempt I made was written directly in [OpenSCAD](http://www.openscad.org/);
# I wrote a small loop to union together a collection of `cube()` calls, one for each slice.
# This had several problems, however.
# First, because I was using cubes it looked very chunky unless the slices were very small.
# Second, I ran into [a bug in OpenSCAD](https://github.com/openscad/openscad/issues/350)
# which causes something like $O(n^2)$ performance for this scenario
# and the file took about 2 hours to render.
# Finally, the STL file it emitted was 1.8 MB and crashed the slicer.
# Clearly, this solution was not going to work.
# Instead, I wrote a python script to output an OpenSCAD file containing a single polyhedron,
# which I could then render into an STL file and hand off to him to slice and print.
# In addition to not crashing the slicer,
# this approach also had the advantage of allowing the resolution to be much coarser
# while still avoiding the 'stair-step' problem of the original multiple `cube()` approach.
import math
import scipy
# ## Setting up
# First, the formulae:
def y1(x): return math.sin(x)
def y2(x): return x*x
# $sin(x) = x^2$ is true for $x = 0$ and $x \approx 0.876$, so that's where I'll start and stop.
START = 0
END = 0.876726
# I'll draw 50 slices, and scale everything up by 30.
SLICES = 50
SCALE = 30
# OpenSCAD's [`polyhedron()` function](https://en.wikibooks.org/wiki/OpenSCAD_User_Manual/Primitive_Solids#polyhedron)
# takes two arguments, `points` and `triangles`.
# (Versions 2014.03 and later can also take `faces` instead of `triangles`, but I'm still using 2014.01.)
# `points` is a list of $[x, y, z]$ triplets, and `triangles` then indexes into the list of points to build the triangles.
# I therefore make a function point(x, y, z)
# which will save the point into the list and return the index into this list.
# Most of the program then works using these indexes, rather than the actual point coordinates.
points = []
def point(x, y, z):
points.append( (x*SCALE,y*SCALE,z*SCALE) )
return len(points)-1
# ## Slicing the shape
# The first step is to slice the shape and get a list of squares.
# (OpenSCAD expects the points on a triangle to be clockwise when looking at them from the outside,
# so throughout the program I maintain this clockwise orientation.) Here's the square; line $\overline{P_2 P_3}$ is the part of the square that sits on the graph. The remainder of the square sits above it.
# I slice the shape into SLICES slices, and output the above square for each slice.
# This is also where I convert the coordinates into point-list indexes as explained above.
def get_slices():
for x in scipy.arange(START, END, (END-START)/SLICES):
yield (
point(x, y1(x), y1(x)-y2(x)),
point(x, y2(x), y1(x)-y2(x)),
point(x, y2(x), 0),
point(x, y1(x), 0),
)
# ## Building the polyhedron
# All of these slices I have are *inside* the shape,
# which isn't the part that's visible.
# The next step is to get all of the faces of the polyhedron
# by connecting the edge of adjoining slices into quadrilaterals.
def get_faces():
slices = list(get_slices())
prev = slices[0]
# First, I make an "end cap" using the slice at the start of the shape.
# This is necessary because otherwise the end will be left 'open' if the first slice is not of size 0,
# and the shape [cannot be exported](https://en.wikibooks.org/wiki/OpenSCAD_User_Manual/STL_Import_and_Export#STL_Export_2)
# because it is not a valid 2-manifold.
yield slices[0]
# Next I generate quadrilaterals conecting each of the sides of ajoining slices.
# Doing this is relatively simple:
# $$
# \mbox{Given slices}
# \substack {
# \square T_0 T_1 T_2 T_3 \\
# \square P_0 P_1 P_2 P_3
# }
# \mbox{, emit faces}
# \substack {
# \square T_0 P_0 P_1 T_1 \\
# \square T_1 P_1 P_2 T_2 \\
# \square T_2 P_2 P_3 T_3 \\
# \square T_3 P_3 P_0 T_0
# }.
# $$
# (Notice that they all go clockwise when facing outward.)
for this in slices[1:]:
def face(a, b): return (
this[a], prev[a],
prev[b], this[b],
)
yield face(0, 1)
yield face(1, 2)
yield face(2, 3)
yield face(3, 0)
prev = this
# The last step in making the polyhedron is to cap off the back end the same as I did with the front end (see above).
yield prev
# ## Convert quadrilaterals into triangles
# I now have a list of faces for the polyhedron. For newer versions of OpenSCAD I could just pass this list in to the `polyhedron()` function; unfortunately as I mentioned before my version of OpenSCAD only accepts a list of triangles.
# Therefore, I take each face (a quadrilateral $\square F_0 F_1 F_2 F_3$) and divide it into two triangles, $\triangle F_0 F_1 F_3$ and $\triangle F_1 F_2 F_3$. (Again, I'm being very careful to keep them in clockwise order.)
def get_triangles():
for face in get_faces():
yield (face[0], face[1], face[3])
yield (face[1], face[2], face[3])
# ## Write the file
# Finally, I print out the OpenSCAD file, which simply consists of a single call to `polyhedron()`:
print "polyhedron("
print " convexity = 1,"
print " triangles = ["
for triangle in get_triangles():
print " [{0}, {1}, {2}],".format(*triangle)
print " ],"
print " points = ["
for point in points:
print " [{0}, {1}, {2}],".format(*point)
print " ]"
print ");"
# And finally, here's what the shape looks like when it's printed out.
# In addition to the Python program linked at the top of this post,
# you can also download
# [the OpenSCAD file](shape.scad) and
# [the STL file](shape.stl).
#  #
# 
 #
# 