Multinomial Probability Mass Function in TI-BASIC
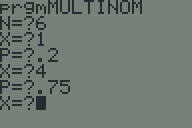
Another TI-BASIC challenge proposed to me by the same person who asked me last time was to calculate the probability mass function of a multinomial distribution. The formula is:
$$\frac{n!}{x_1 \cdots x_k} p_1^{x_1}\cdots p_k^{x\_k}
\mbox{ where }
n = \sum\_{i=1}^k x_i$$
The naïve way of calculating this is to read
$x\_1$ and $p\_1$ through $x\_k$ and $p\_k$ and then crunch the numbers.
However, this necessitates a list to keep track of all the numbers and
an extra loop at the end to crunch them. Since we don't actually need
the numbers, there's an easier way.
Calculating the mode of a list in TI-BASIC
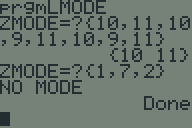
Recently, someone challenged me to write a program to find the mode (or modes) of a list in TI-BASIC. I picked up my TI-83+ and whipped this program up in about half an hour. Somebody else asked me for a copy, so I figured I'd post it on my website.