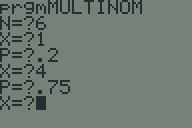
Another TI-BASIC challenge proposed to me by the same person who asked me
last time was to calculate the
probability mass function of a multinomial distribution. The formula is:
$$\frac{n!}{x_1 \cdots x_k} p_1^{x_1}\cdots p_k^{x_k}
\mbox{ where }
n = \sum_{i=1}^k x_i$$
The naïve way of calculating this is to read
$x_1$ and $p_1$ through $x_k$ and $p_k$ and then crunch the numbers.
However, this necessitates a list to keep track of all the numbers and
an extra loop at the end to crunch them. Since we don’t actually need
the numbers, there’s an easier way.
How it works
This formula can be broken down into three basic parts:
$$\begin{align}
numerator &= n! \\\\
denominator &= x_1 \cdots x_k \\\\
multiplier &= p_1^{x_1}\cdots p_k^{x_k}
\end{align}$$
For each $i$, $x_i$ and $p_i$ are read, and the new values of $numerator$
and $denominator$ are calculated. Once this is done, $x_i$ and $p_i$ are no longer needed.
Finally, once all of the numbers have been read in, the final answer is just
$$\frac{n!}{denominator}multiplier$$
This program also does some sanity checking to make sure that
$\sum_{i=1}^k p_i = 1$ and $\sum_{i=1}^k x_i = n$.
Variables used
N | $n$ |
D | $denominator$ ($x_1 \cdots x_k$) |
M | $multiplier$ ($p_1^{x_1}\cdots p_k^{x_k}$) |
P | $p\_i$ |
O | $\sum_{i=1}^k p_i$ |
X | $x\_i$ |
W | $\sum_{i=1}^k x_i$ |
The Program
Download: MULTINOM.8Xp
Prompt N
1→D:1→M:0→O:0→W:1→X
While X≠0
Prompt X
If X≠0:Then
Prompt P
X+W→W:P+O→O
D*(X!)→D
M*(P^X)→M
End:End
If O≠1:Then
Disp "E: sum(P)≠1
Stop:End
If W≠N:Then
Disp "E: sum(X)≠N
Stop:End
((N!)/D)*M
Example
In a recent three-way election for a large country, candidate A received 20% of the votes, candidate B received 30% of the votes, and candidate C received 50% of the votes. If six voters are selected randomly, what is the probability that there will be exactly one supporter for candidate A, two supporters for candidate B and three supporters for candidate C in the sample?
(source)
To find the solution using prgmMULTINOM:
N=?6 | Number of supporters (1+2+3) |
X=?1 | Supporters for candidate A |
P=?.2 | Votes for candidate A |
X=?2 | Supporters for candidate B |
P=?.3 | Votes for candidate B |
X=?3 | Supporters for candidate C |
P=?.5 | Votes for candidate C |
X=?0 | End of input |
.135 | Result |
Update December 2015: Added example of how to use the program, since I couldn’t remember how myself.