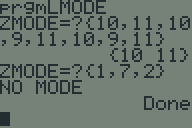
Recently, someone challenged me to write a program to find the mode (or modes) of a list in TI-BASIC. I picked up my TI-83+ and whipped this program up in about half an hour. Somebody else asked me for a copy, so I figured I'd post it on my website.
How it works
The program operates in two passes. For the first pass, it finds how many times the most frequent number appears. This is facilitated by grouping the numbers by sorting them, so only one number needs to be counted at a time.
Once it has found the number of times the numbers of the mode appears, it passes through the list a second time and moves all of the numbers of the mode into an output list.
Variables used
LZMODE |
Input list. Will be sorted in ascending order. |
LMODE |
Output list. Contains the modes of LZMODE. |
I |
Generic counter variable, used in For loops. |
C |
(for Count) How many times the current number (stored
in N) has appeared so far. |
N |
The current number being counted. |
M |
(For Max) How large the largest C has been so far. |
D |
(For Dim) For pass 2, the current position in LMODE. |
The Program
Download: LMODE.8Xp
Prompt LZMODE
SortA(LZMODE
0→C:0→M:LZMODE(1)→N
For(I,1,dim(LZMODE
If LZMODE(I)=N:Then
C+1→C
Else
If C>M:C→M
1→C
LZMODE(I)→N
End:End
If C>M:C→M
"PASS 2
If M=1:Then
Disp "NO MODE"
Return:End
0→C:LZMODE(1)→N:1→D:{0}→LMODE
For(I,1,dim(LZMODE
If LZMODE(I)=N:Then
C+1→C
Else
If C=M:Then
N→LMODE(D):D+1→D:End
LZMODE(I)→N
1→C
End:End
If C=M:N→LMODE(D
"RETURN":LMODE
Update December 2015: The original version of this program had a bug: if the largest number in the list was a mode of that list, it would not be included in the output. For example, if the list was
{4, 3, 4}the program would outputNO MODEinstead of{4}.I discovered this problem right after I wrote this post, and simply worked around it thereafter. However it's been bugging me ever since and I finally sat down and fixed it.