Rendering a 3D shape with Python

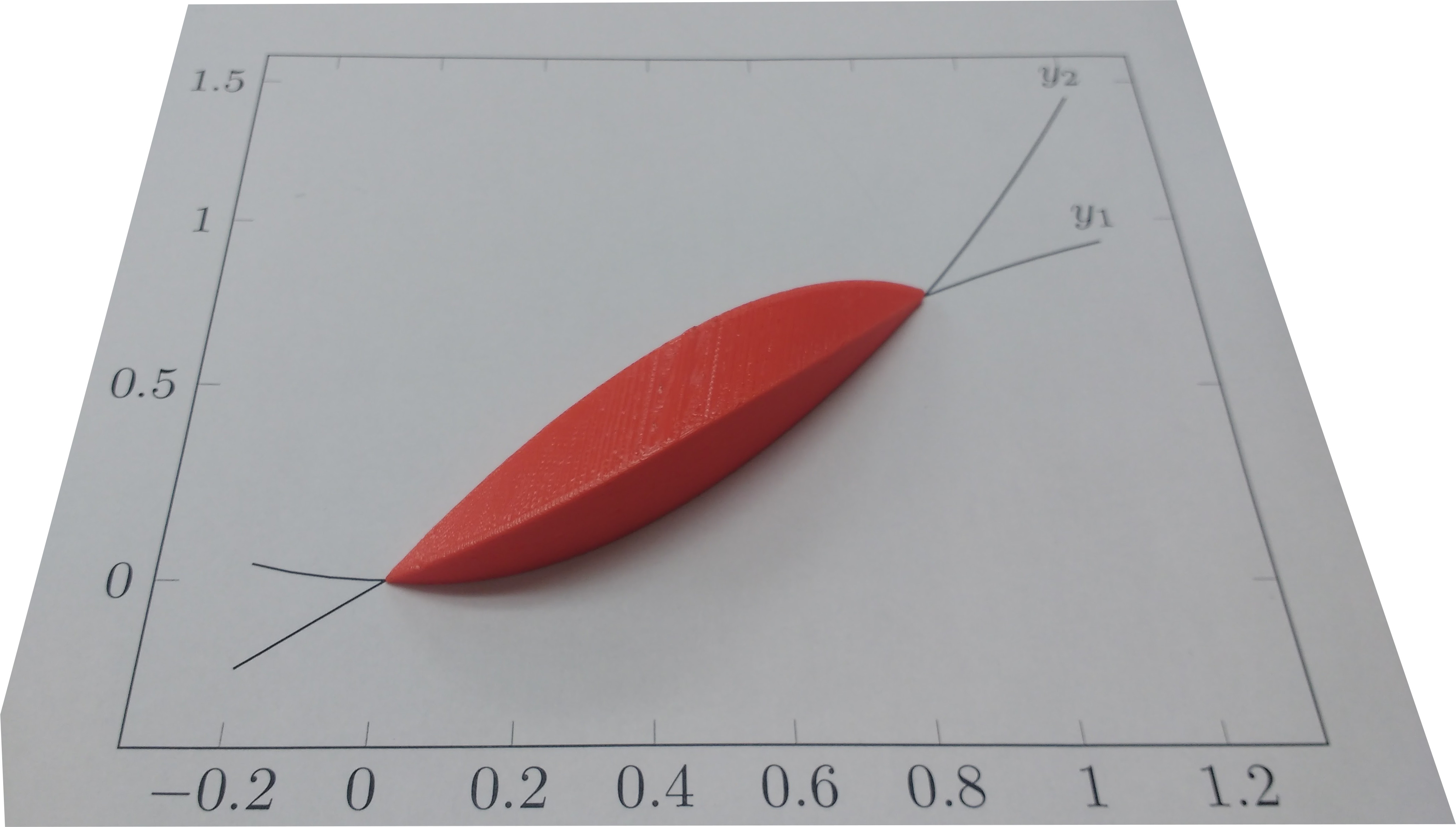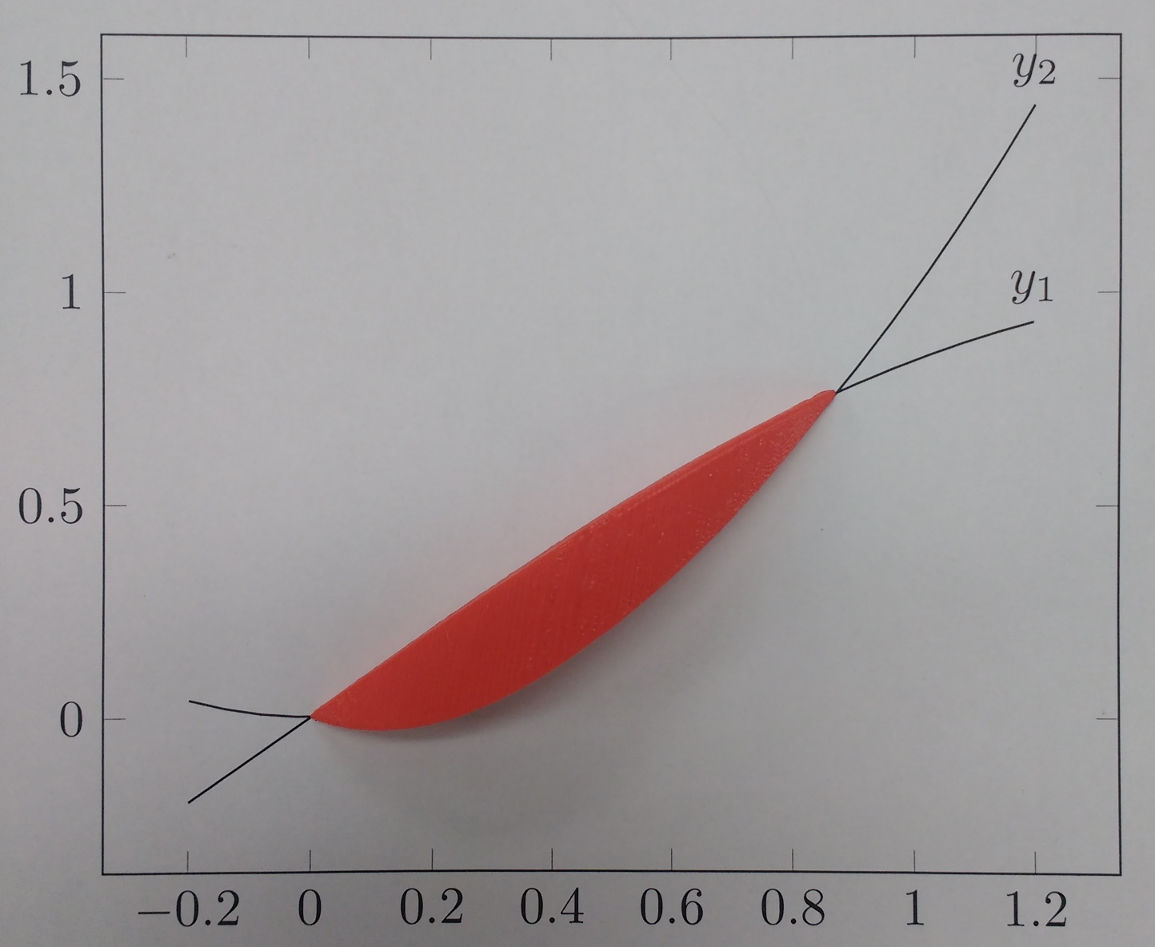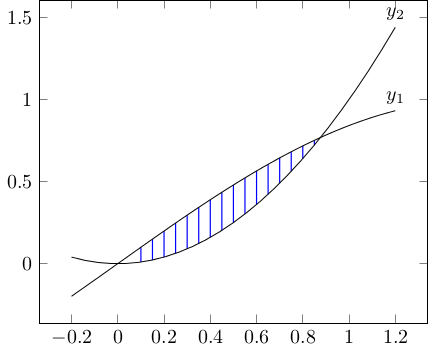
A friend wanted to 3D-print a shape to demonstrate using calculus to find the volume of solids of known cross-section. The shape he wanted was a graph of $sin(x)$ vs $x^2$, where each vertical slice of the intersection was a square. Here's the graph, with $y_1 = sin(x)$ and $y_2 = x^2$. The blue lines show the edge of each square. He couldn't figure out how to do this in a CAD program (I'm not even sure if it's possible), so he asked me if I could write some code to render it.

This post was written in literate Python. Download buildshape.py and run it yourself!

The first attempt I made was written directly in OpenSCAD; I wrote a small loop to union together a collection of cube() calls, one for each slice. This had several problems, however. First, because I was using cubes it looked very chunky unless the slices were very small. Second, I ran into a bug in OpenSCAD which causes something like $O(n^2)$ performance for this scenario and the file took about 2 hours to render. Finally, the STL file it emitted was 1.8 MB and crashed the slicer.

Clearly, this solution was not going to work. Instead, I wrote a python script to output an OpenSCAD file containing a single polyhedron, which I could then render into an STL file and hand off to him to slice and print. In addition to not crashing the slicer, this approach also had the advantage of allowing the resolution to be much coarser while still avoiding the 'stair-step' problem of the original multiple cube() approach.

Setting up

First, the formulae:

38
39

def y1(x): return math.sin(x)
def y2(x): return x*x

$sin(x) = x^2$ is true for $x = 0$ and $x \approx 0.876$, so that's where I'll start and stop.

42
43

START = 0
END = 0.876726

I'll draw 50 slices, and scale everything up by 30.

46
47

SLICES = 50
SCALE = 30

OpenSCAD's polyhedron() function takes two arguments, points and triangles. (Versions 2014.03 and later can also take faces instead of triangles, but I'm still using 2014.01.) points is a list of $[x, y, z]$ triplets, and triangles then indexes into the list of points to build the triangles. I therefore make a function point(x, y, z) which will save the point into the list and return the index into this list. Most of the program then works using these indexes, rather than the actual point coordinates.

points = []
def point(x, y, z):
	points.append( (x*SCALE,y*SCALE,z*SCALE) )
	return len(points)-1

Slicing the shape

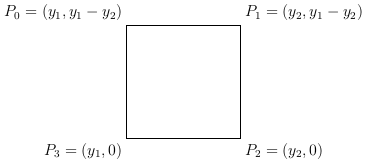
The first step is to slice the shape and get a list of squares. (OpenSCAD expects the points on a triangle to be clockwise when looking at them from the outside, so throughout the program I maintain this clockwise orientation.) Here's the square; line $\overline{P_2 P_3}$ is the part of the square that sits on the graph. The remainder of the square sits above it.

I slice the shape into SLICES slices, and output the above square for each slice. This is also where I convert the coordinates into point-list indexes as explained above.

def get_slices():
	for x in scipy.arange(START, END, (END-START)/SLICES):
		yield (
			point(x, y1(x), y1(x)-y2(x)),
			point(x, y2(x), y1(x)-y2(x)),
			point(x, y2(x), 0),
			point(x, y1(x), 0),
		)

Building the polyhedron

All of these slices I have are inside the shape, which isn't the part that's visible. The next step is to get all of the faces of the polyhedron by connecting the edge of adjoining slices into quadrilaterals.

First, I make an "end cap" using the slice at the start of the shape. This is necessary because otherwise the end will be left 'open' if the first slice is not of size 0, and the shape cannot be exported because it is not a valid 2-manifold.

90	`yield slices[0]`

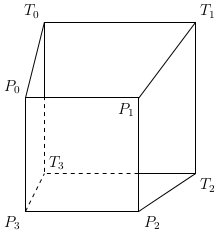
Next I generate quadrilaterals conecting each of the sides of ajoining slices. Doing this is relatively simple:

$$ \mbox{Given slices} \substack { \square T_0 T_1 T_2 T_3 \\ \square P_0 P_1 P_2 P_3 } \mbox{, emit faces} \substack { \square T_0 P_0 P_1 T_1 \\ \square T_1 P_1 P_2 T_2 \\ \square T_2 P_2 P_3 T_3 \\ \square T_3 P_3 P_0 T_0 }. $$

(Notice that they all go clockwise when facing outward.)

for this in slices[1:]:
		def face(a, b): return (
			this[a], prev[a],
			prev[b], this[b],
		)
		yield face(0, 1)
		yield face(1, 2)
		yield face(2, 3)
		yield face(3, 0)
		prev = this

The last step in making the polyhedron is to cap off the back end the same as I did with the front end (see above).

122	`yield prev`

Convert quadrilaterals into triangles

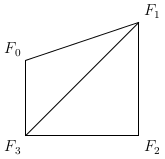
I now have a list of faces for the polyhedron. For newer versions of OpenSCAD I could just pass this list in to the polyhedron() function; unfortunately as I mentioned before my version of OpenSCAD only accepts a list of triangles. Therefore, I take each face (a quadrilateral $\square F_0 F_1 F_2 F_3$) and divide it into two triangles, $\triangle F_0 F_1 F_3$ and $\triangle F_1 F_2 F_3$. (Again, I'm being very careful to keep them in clockwise order.)

def get_triangles():
	for face in get_faces():
		yield (face[0], face[1], face[3])
		yield (face[1], face[2], face[3])

Write the file

Finally, I print out the OpenSCAD file, which simply consists of a single call to polyhedron():

print "polyhedron("
print "	convexity = 1,"
print "	triangles = ["
for triangle in get_triangles():
	print "		[{0}, {1}, {2}],".format(*triangle)
print "	],"
print "	points = ["
for point in points:
	print "		[{0}, {1}, {2}],".format(*point)
print "	]"
print ");"

And finally, here's what the shape looks like when it's printed out. In addition to the Python program linked at the top of this post, you can also download the OpenSCAD file and the STL file.